背景
Matrix67有这么一篇文章:原来函数也是有平方根的,讲述了一个有趣的构造,给出了满足$f(f(x))=e^x$的函数$f$。然而美中不足的是这个函数是分段的,所以评论区有个老哥试图给出一种离散的解决方案。然而他失败了,他给出的函数显然不满足要求(考虑$f(f(0))$,它应该$=1$,然而现在$f(f(0))=f(\ln{2})>\ln{2}+1\times \ln{2}^{1}>1$,矛盾)。
所以这个神奇的有理数序列是如何得出的呢?我百思不得其解,只好上OEIS一探究竟。还真叫我搜到了,这个序列是A052105,原来是$f(f(x))=e^x-1$的解$f$的级数表达。
求解过程
这样我就知道它的求解方式了:因为$e^x-1$没有常数项,这个多项式复合函数是良定义的,可以只算有限项而不必考虑无穷级数的事。于是我很快就写出了一个$O(n\times \textrm{多项式复合函数})=O(n^4)$的垃圾算法求前$n$项系数的值。
设$f(x)=\sum{a_kx^k}$。对于$n>1$,我们有如下的推导:
\[[x^n]\sum_{i=1}^{n}a_i\left(\sum_{j=1}^{n}a_jx^j\right)^i=\frac{1}{n!}\] \[[x^n]\left(\sum_{i=1}^{n-1}a_i\left(\sum_{j=1}^{n}a_jx^j\right)^i\right)+a_na_1^n=\frac{1}{n!}\] \[[x^n]\left(a_1\left(\sum_{j=1}^{n}a_jx^j\right)+\sum_{i=2}^{n-1}a_i\left(\sum_{j=1}^{n-1}a_jx^j\right)^i\right)+a_na_1^n=\frac{1}{n!}\] \[(a_1+a_1^n)a_n+[x^n]\left(\sum_{i=2}^{n-1}a_i\left(\sum_{j=1}^{n-1}a_jx^j\right)^i\right)=\frac{1}{n!}\]这样我们就用前$n-1$项的系数求出了$a_n$。
最后我们只需要确定第一项的系数就行了。显然只有$\pm{1}$这两种可能,但是$-1$会让第二项的计算过程除0,所以必须取$a_1=1$作为初始条件。
效果
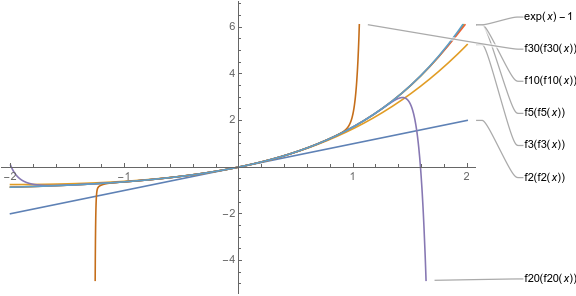
这样子计算出来的函数一开始表现得非常正常,然而多算几项就会发现实际上它不会收敛,算到50项左右时系数就已经变成天文数字了。所以很可惜,这个函数仅满足对任意$n$,$f(f(x))\equiv e^x-1 \pmod{x^n}$,但是对于任意$x\ne 0$都不满足$f(f(x))=e^x-1$;甚至实际上对于任意$x\ne 0$,$f(x)$会趋近于$\pm{\infty}$。
用Mathematica画了几张图表现一下近似的效果,$f_n(x)$表示取前$n$项的函数,可见取$5$项左右的效果是最好的:
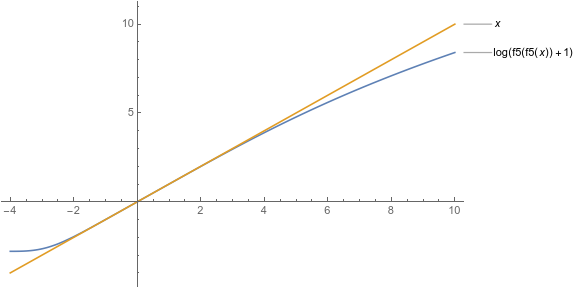
拓展
明显这是一个通法,对于任意一个可在某点处泰勒展开且无常数项的函数,都可以求出一个对应的$f$。
比如对于$f(f(x))=\sin{x}$:
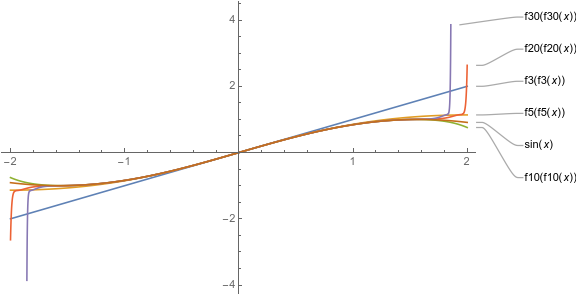
这次系数貌似到前50项都是收敛的,然而再多算几项就会发现实际上还是发散的。
对于$f(f(x))=\ln{(x+1)}$:
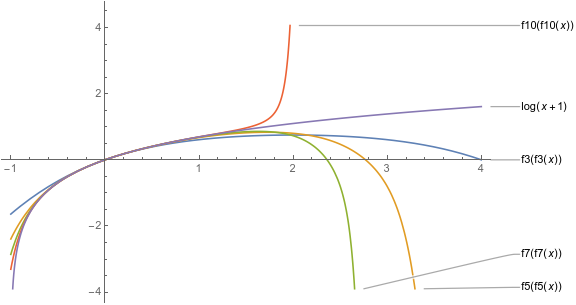
这个发散得特别快。
对于$f(f(x))=\exp{(e^x-1)}-1$(右边是贝尔数的EGF$-1$):
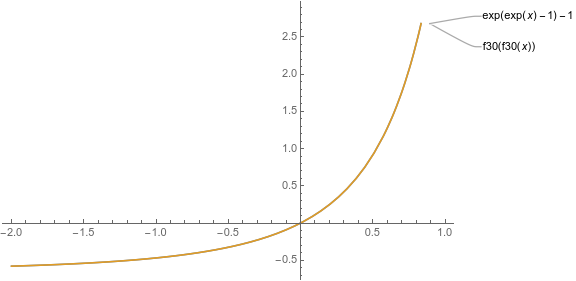
可知其可以得到正确答案$f(x)=e^x-1$。所以我大胆猜想:只要满足条件的$f(x)$存在,这个算法就一定可以求出;前面那些例子求不出是因为答案$f(x)$在$0$处的泰勒展开的收敛半径是零。
关于我是怎么绘图的
首先我写了个Rust程序来算前$30$项的系数。同时我使用isympy算出用有理数表示的系数,进行验算。
然后我用如下的mathematica命令得到$f_n(x)$:
makePoly = Function @@ {l, Function @@ {x, Internal`FromCoefficientList[l, x]} }
makePolyN = Function @@ { {n, l}, makePoly[Drop[l, n - 30]]}
l = {你的列表}
f3 = makePolyN[3, l]
f5 = makePolyN[5, l]
f10 = makePolyN[10, l]
...
接着用如下的命令来画这若干个$f_n(x)$:
Plot[{f30[f30[x]], ..., Exp[Exp[x] - 1] - 1}, {x, -2, 1}, PlotLabels -> "Expressions"]
可惜prism.js不支持wolfram语言的高亮。