简介
sympy是一个符号计算的python库。他不仅可以像mathematica一样进行符号计算,也内置了很多的OI实用算法,包括图论、计算几何、数论、多项式等等很多方面。可以节省您码板子的时间。
前置知识
- 基本python语法
- 一定的数学能力
安装方法
pip install sympy ipython
如果还没有安装pip的话,在Ubuntu中可以sudo apt install python3-pip,否则请自行百度pip安装方法。
然后在终端中输入isympy回车,就打开了一个使用IPython界面的sympy。
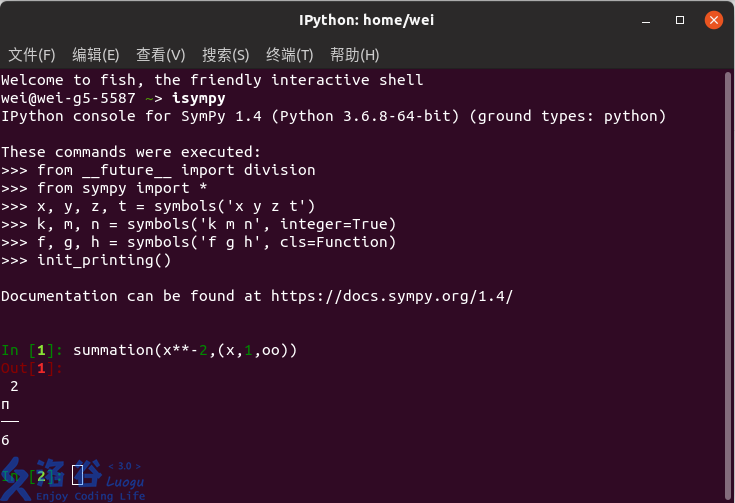
虽然本文中的ascii art可能稍有变形,但是Linux下终端里是不会变形的。 Windows不能够正确排版,但是仍然可以使用print输出。
直接在函数名后加上?,即可查询函数用法。加??可以查看源代码。
函数名以及参数可以打Tab自动补全。
使用cxxcode(s)即可把SymPy表达式s转为C++语言的表达式。
使用sympify(s)即可把字符串s转为SymPy的表达式,比如说把"x^y"替换为x**y,把"8/10"计算为有理数类型的4/5而非浮点数0.8。
使用plot(f)绘制函数f的图像。后面可以接一个区间,比如plot(x**x,(x,0,1))表示\(x^x,x\in[0,1]\)
基本用法
如求导、积分、级数求和、极限、因式分解、解微分方程等等。
参见官方英文教程和较老的中文教程,可以代替Wolfram|Alpha的大部分功能。
数论的函数
再次强调在函数名后加上?(比如sum?),即可查看函数的用法,大多数的函数还有示例,所以下文不会介绍函数的参数。
isprime:判质数,用的是Miller-Rabinnextprime(n):\(\ge n\)的最小质数,和mathematica里同名函数表现相同primepi(n):求n以内质数个数,用的是Min_25筛的第二部分,可以在源码中看到优美的Min_25筛实现。pollard_rho:可以指定自己的伪随机函数和种子gcdex:整数或者多项式的exgcdprimitive_root:最小原根mod_inverse:求逆discrete_log:离散对数sqrt_mod:模意义下开方diophantine:解各种丢番图方程,比如佩尔方程:
In [35]: diophantine(x*x-2*y*y-1)
Out[35]:
⎧⎛ t t
⎪⎜ t 3⋅(3 - 2⋅√2) t 3⋅(2⋅√2 + 3)
⎨⎜- √2⋅(3 - 2⋅√2) + ───────────── + √2⋅(2⋅√2 + 3) + ─────────────, - (3 - 2⋅
⎪⎝ 2 2
⎩
t t ⎞ ⎛ t
t 3⋅√2⋅(3 - 2⋅√2) 3⋅√2⋅(2⋅√2 + 3) t⎟ ⎜ 3⋅(3 - 2⋅√2)
√2) + ──────────────── - ──────────────── - (2⋅√2 + 3) ⎟, ⎜- ───────────── +
4 4 ⎠ ⎝ 2
t t
t 3⋅(2⋅√2 + 3) t 3⋅√2⋅(3 - 2⋅√2)
√2⋅(3 - 2⋅√2) - ───────────── - √2⋅(2⋅√2 + 3) , - ──────────────── + (3 - 2⋅√
2 4
t⎞⎫
t t 3⋅√2⋅(2⋅√2 + 3) ⎟⎪
2) + (2⋅√2 + 3) + ────────────────⎟⎬
4 ⎠⎪
⎭
egyptian_fraction:埃及分数
各种数
fibonacci:fibonacci数catalan:catalan数npartitions:整数拆分函数,就算n=1e8都可以秒出,难以置信rf:上升幂ff:下降幂binomial:组合数bell:Bell数bernoulli:伯努利数
多项式操作
div:多项式除法、取模ntt,intt:NTTfft,ifft:FFTfwht,ifwht:异或的FWTmobius_transform,inverse_mobius_transform:FMT,如果设置了subset=False的话是AND的FWT
什么多项式exp,多项式ln,多项式求逆之类的,可以使用series,如下:
In [77]: exp(1/(log(2*x**2+3*x+1)+5*x+1)-1).series(x,0,5)
Out[77]:
2 3 4
197⋅x 3517⋅x 326023⋅x ⎛ 5⎞
1 - 8⋅x + ────── - ─────── + ───────── + O⎝x ⎠
2 3 24
计数题乱搞专用
interpolate:拉格朗日插值rational_interpolate:有理式插值,直接秒掉概率论这样的题
参数是一个\((x,y)\)列表,然后是分子的次数(这个可能要手动枚举)
In [134]: R=Rational #总是输入Rational太长了
In [135]: rational_interpolate([(1,1),(2,1),(3,R(6)/5),(4,R(10)/7)],2)
Out[135]:
2
x x
── + ─
4 4
───────
x - 1/2
rsolve_hyper:非常系数非齐次线性递推求通项
第一个参数是一个列表l,第二个参数是函数f,第三参数是变量n,返回\(\sum_{k=0}^{len(l)-1}l_kF(n+k)=f(n)\)的解\(F\)。
In [83]: rsolve_hyper([-4,4,-1],0,n) #有重根的线性递推
Out[83]:
n
2 ⋅(C₀ + C₁⋅n)
In [94]: rsolve_hyper([-4*n-2,n+2],0,n) #卡特兰数
Out[94]:
n
4 ⋅C₀⋅RisingFactorial(1/2, n)
─────────────────────────────
RisingFactorial(2, n)
In [87]: rsolve_hyper([-1,-1,1],0,n) #斐波那契数
Out[87]:
n n
⎛1 √5⎞ ⎛1 √5⎞
C₀⋅⎜─ - ──⎟ + C₁⋅⎜─ + ──⎟
⎝2 2 ⎠ ⎝2 2 ⎠
In [90]: rsolve_hyper([-1,1],1+n,n) #可以用来求前缀和
Out[90]:
n⋅(n + 1)
C₀ + ─────────
2
计算几何
Circle、Line、Line3D、Point、Point3D:各种几何对象convex_hull:求凸包centroid:求重心farthest_points:最远点对closest_points:最近点对
线性代数
注:大部分的功能numpy已经具备,并且效率远高于sympy,所以这里只介绍numpy没有或者不完善的功能
Matrix:矩阵类,构造方法类似numpy的arraydet(m):求m行列式,可以带变量,所以能用来求特征多项式之类的,如下:
In [109]: m=Matrix([[0,1,0],[0,0,1],[1,1,1]])
In [110]: det(x*eye(3)-m)
Out[110]:
2
x ⋅(x - 1) - x - 1
m.inv_mod(p):求mod p意义下m的逆矩阵m.exp():矩阵指数,用封闭形式表示结果m.eigenvals(),m.eigenvects():特征值、特征向量,可以用根式表示结果
图论
sympy此方面功能不多。
topological_sort:拓扑序combinatorics.prufer.Prufer.to_prufer:树转prufer序列combinatorics.prufer.Prufer.to_tree:prufer序列转树
彩蛋:数学作业用法
举几个比较初等的例子,可能对数学作业稍有帮助:
三角函数化简,求周期之类的
In [13]: trigsimp(sin(x)+sqrt(3)*cos(x))
Out[13]:
⎛ π⎞
2⋅sin⎜x + ─⎟
⎝ 3⎠
In [14]: expand_trig(cos(2*x+pi/2))
Out[14]: -2⋅sin(x)⋅cos(x)
In [17]: periodicity(exp(cos(x/3+1)+sin(x)),x)
Out[17]: 6⋅π
待定系数法,这里是把斐波那契数拆成两个等比级数之和:
In [31]: solve_undetermined_coeffs(Eq(c/(1-a*x)+d/(1-b*x),1/(1-x-x**2)),[a,b,c,d
...: ],x)
Out[31]:
⎡⎛1 √5 1 √5 1 √5 √5 1⎞ ⎛1 √5 1 √5 √5 1 1 √5⎞⎤
⎢⎜─ - ──, ─ + ──, ─ - ──, ── + ─⎟, ⎜─ + ──, ─ - ──, ── + ─, ─ - ──⎟⎥
⎣⎝2 2 2 2 2 10 10 2⎠ ⎝2 2 2 2 10 2 2 10⎠⎦
高次方程判别式:
In [29]: discriminant(x**7-x-1)
Out[29]: -776887
In [30]: discriminant(x**2+4*x+4)
Out[30]: 0
还有一些Parabola、Ellipse之类的圆锥曲线类,我因为不懂圆锥曲线所以不会用。