今天看到YouTube上有这么一个视频,觉得超有意思,于是把它加到了chrome收藏的首位。
视频大概讲的是一个叫做PPS的自组织系统。这个自组织系统的规则非常简单,和conway的生命游戏一样简单。尽管不能像生命游戏一样做出模拟图灵机那样的神仙构造,但是它无疑更加接近生命的形式。“细胞”可以吸收周围的营养而生长,繁殖“孢子”或者自我分裂,与别的细胞物质交流,当然还有死亡。如果觉得这么描述太过扯淡了的话,也可以想象成一个可以分裂、合并、插入、删除、垃圾回收的splay森林(???)。
系统的规则是这样的:
- 有\(n\)个粒子,每个粒子有一个位置\((x,y)\)和朝向\(\phi\)。所有粒子有一个共同的速率\(v\)。
- 一个粒子受到周围距离\(r\)之内粒子的影响。
- 系统以“秒”为单位演化。每一秒钟,所有粒子同时统计出(他朝向的)两侧影响他的粒子数\(L\)和\(R\),然后赋值\(\theta\leftarrow\theta+\alpha+\beta(L+R)\mathrm{sgn}(L-R)\)。其中\(\alpha\),\(\beta\)是两个常数,\(\mathrm{sgn}(x)=\frac{x}{\vert x\vert}\)。
- 下一秒钟粒子的位置由当前的\(\theta\)和\(v\)决定。就是简单的物理计算。
因为放寒假很无聊,我就试着手工实现了一下这个系统。代码还是超级简单的,只是一直得不到预想的效果。最后发现我智障的把\(180^\circ\)写成了\(\frac{\pi}{2}\)。
因为我不知道ubuntu怎么截屏截成视频,就只放了几张截图,难以表现让人感到震撼的生命的演化历程。图中\(L+R\)越大,粒子的颜色越亮。
下面这张是视频里的例子,\(\alpha=180^\circ\),\(\beta=17^\circ\)。中间的几个小球是“孢子”,左下角是一个典型的细胞(内外两层,可以呈现环状或者多边形,这个是三角形的)。
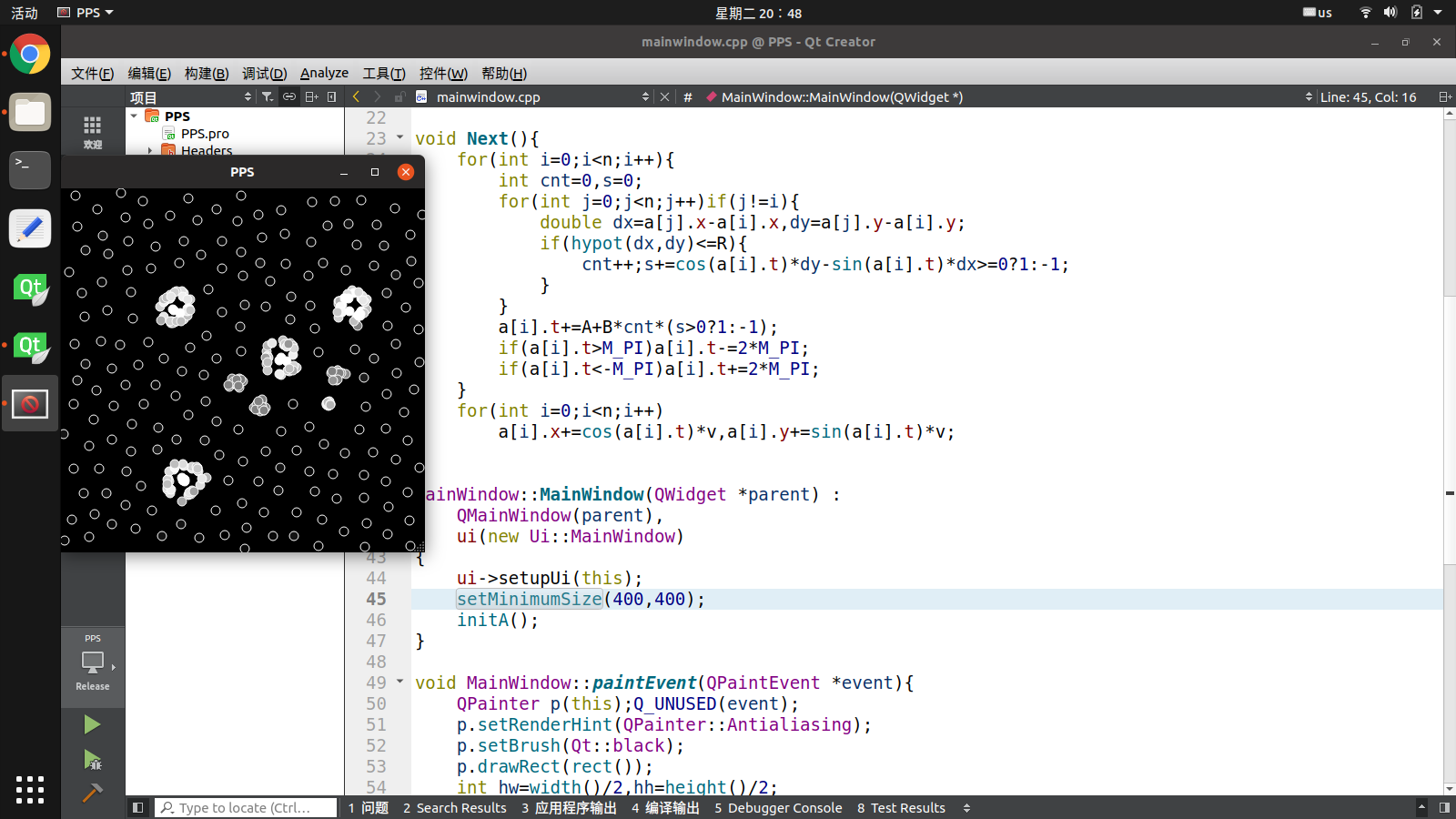
然后是\(\alpha=-159^\circ\),\(\beta=15^\circ\)。图中只有一个处于生命末期的细胞,已经成五边形了。很少看见一直成长到六边形的细胞。
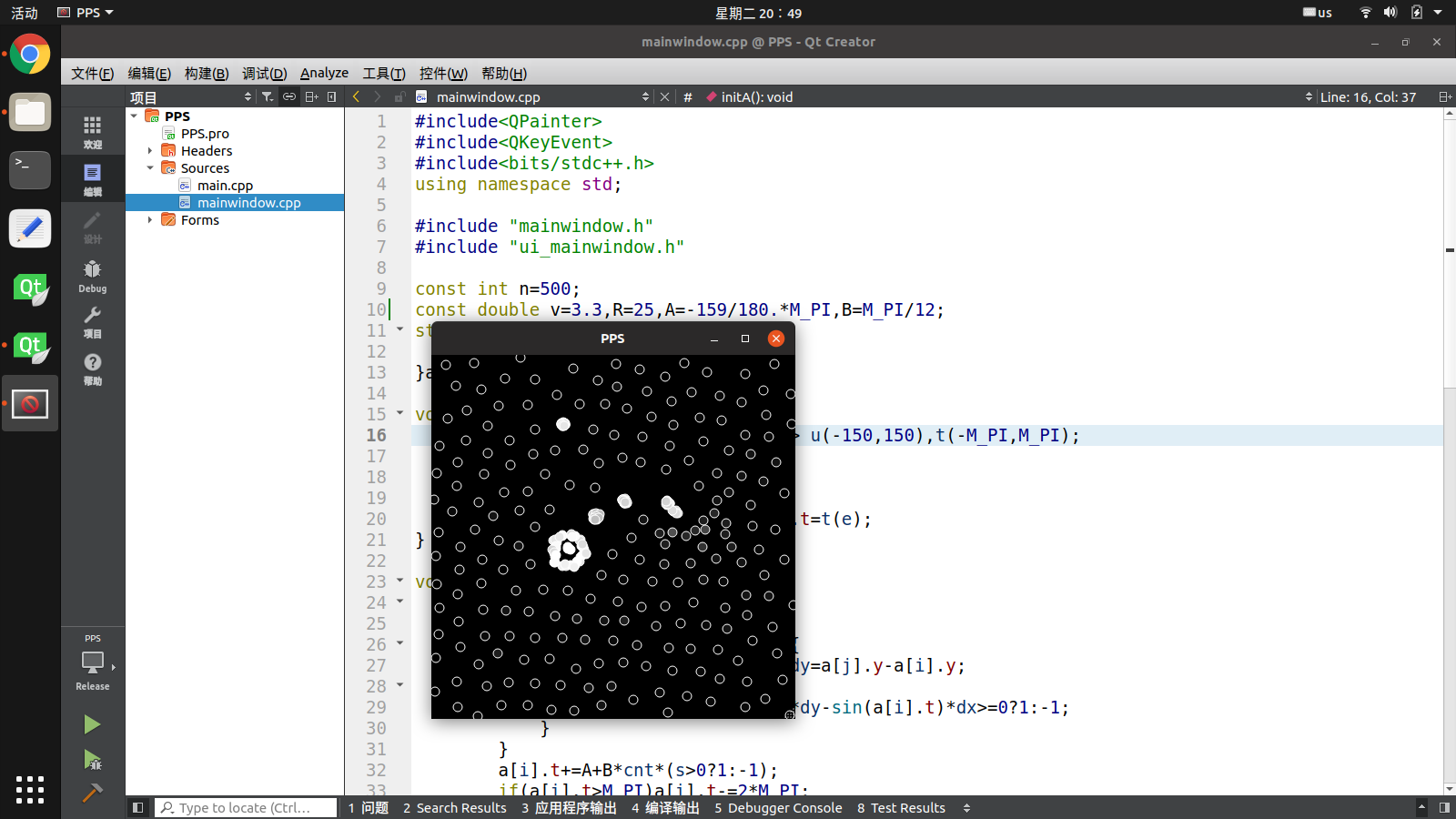
WARNING : 请自动忽略下图中的政治敏感内容!
下面的参数就不能形成生命了。这是\(\alpha=45^\circ\),\(\beta=4^\circ\),只能形成很厚的死细胞(不能进行物质交流、产生孢子之类的生命活动)。
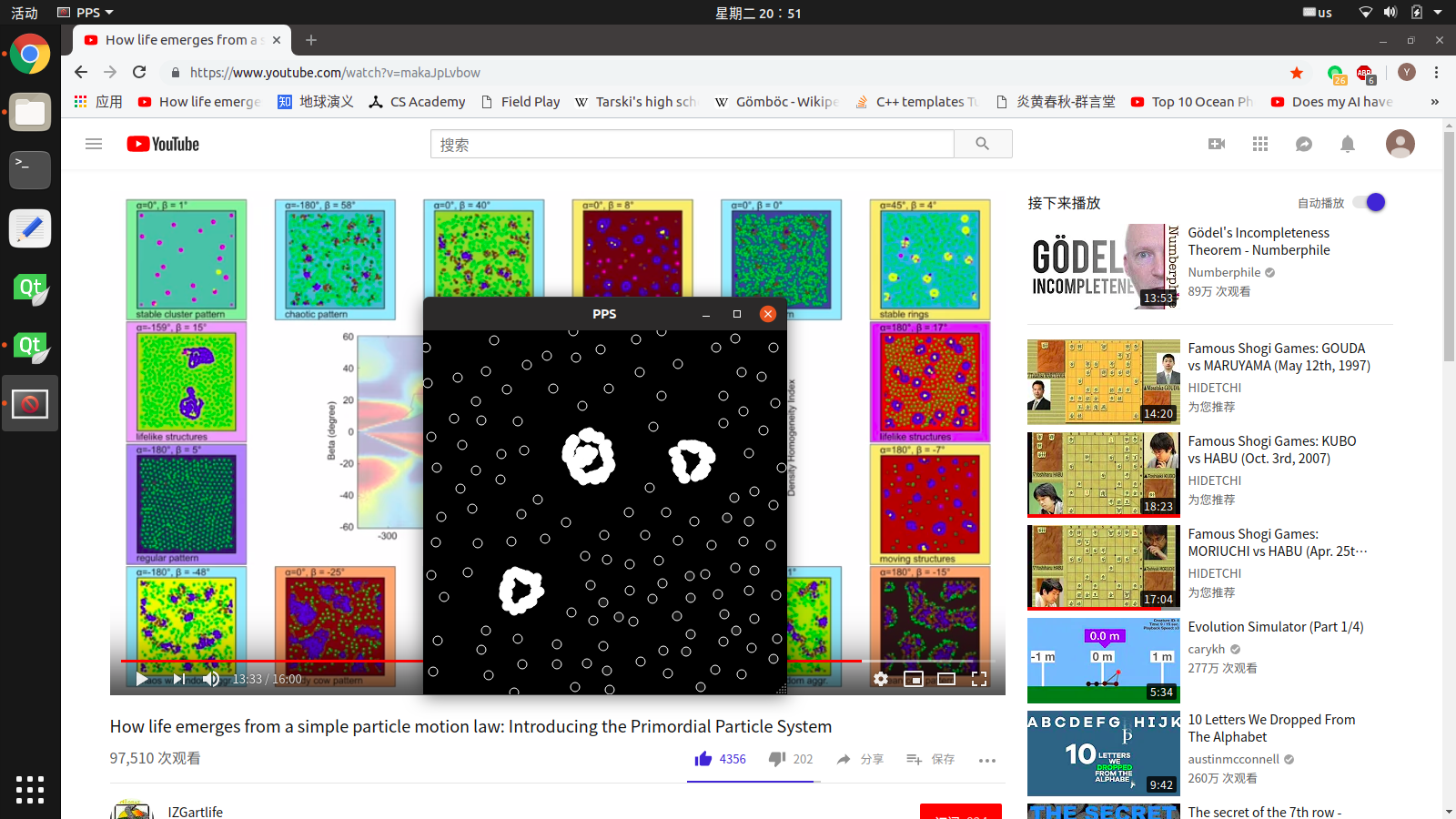
最后一张是\(\alpha=180^\circ\),\(\beta=-15^\circ\)。这里不能形成任何的组织,只能形成一团可怕的变形虫一样的物体。截图不能表现出来它的特点。
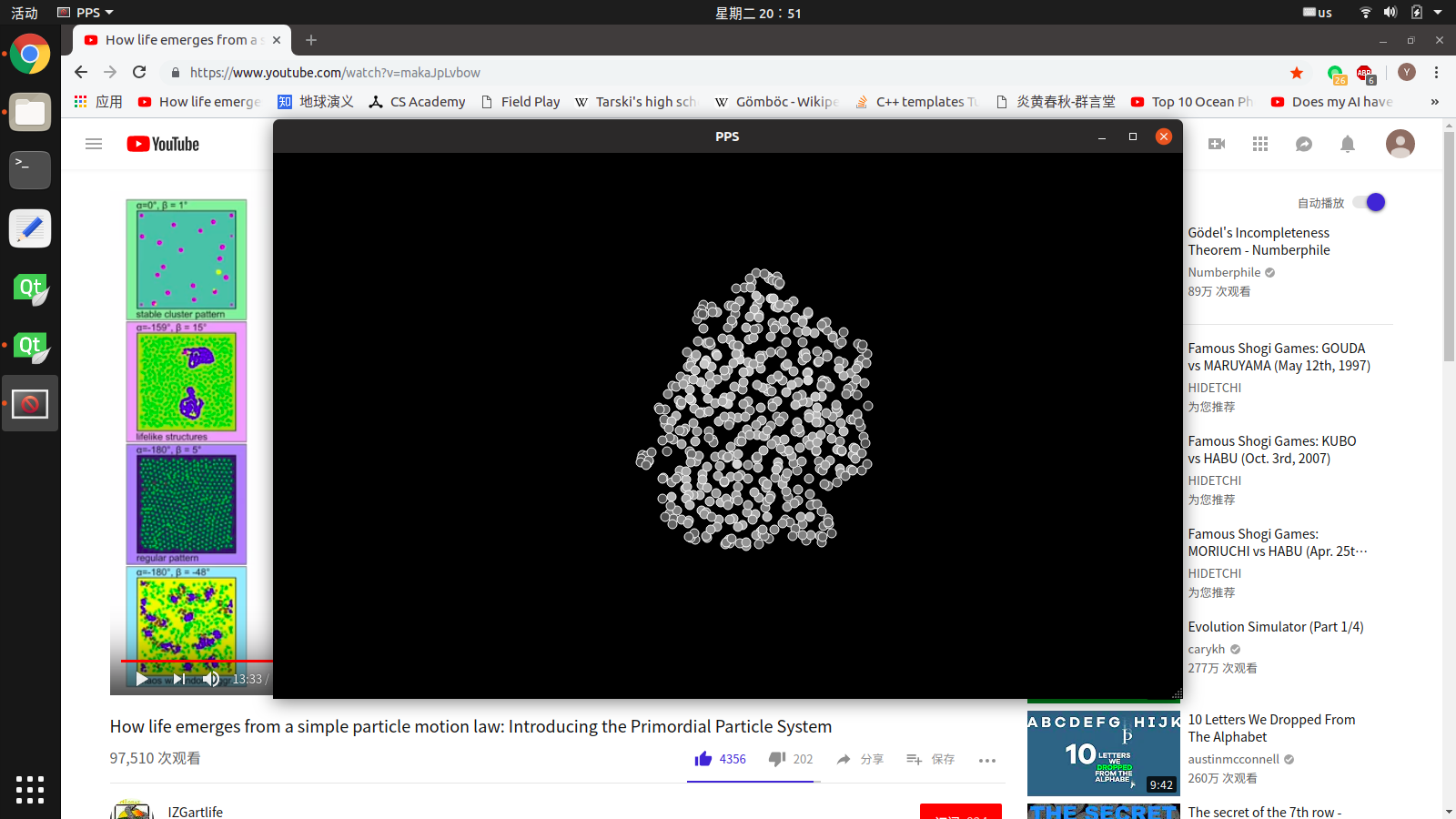
懒得贴代码了,在此推广我的代码仓库,可以自行clone。